Logistic regression is a powerful and versatile statistical technique that has been widely used in various fields, including machine learning, statistics, and social sciences. It is a simple yet effective method for modeling the relationship between a binary response variable and one or more predictor variables.
The beauty of logistic regression lies in its ability to provide interpretable results, while still being flexible enough to handle complex data. By analyzing the coefficients of the model, we can gain insights into the factors that are driving the outcomes of interest and make informed decisions based on these insights.
Logistic Regression - Demolished
Logistic regression is a process of modelling the probability of a discrete outcome given an input variable. The most common logistic regression models a binary outcome; something that can take two values such as true/false, yes/no, 1/0 and so on.
- Training data: $N$ training examples of a $D$-dimensional input data.
where, \(\mathbf{x}_{i}\) = \(\begin{pmatrix} x_{1}^{(i)} \\ x_{2}^{(i)} \\ \vdots \\ x_{N}^{(i)} \end{pmatrix}\) , \(i=1,2, \dots, D\).
- Response: Binary-valued target of the corresponding $N$ training examples:
The input data $\mathbf{x}_{i}, \space i=1,2, \dots, D$ are know as variables and they can come from different sources:
- quantitative inputs (e.g. Income, Age, etc.)
- basis function, e.g. $\phi_{j}=\mathbf{x}^{j}$ (polynomial regression)
- numeric or “dummy” encodings of qualitative inputs
- interactions between variables, e.g. $\mathbf{x_{1}}=\mathbf{x_{2}} \cdot \mathbf{x_{3}}$
and we assume that these data points are drawn independently from the population distribution.
Mathematical Formula
The simplest form of Linear Regression model as seen in the previoys post is linear functions of the input variables:
\[\hat{y} = f(\mathbf{x}, \mathbf{w}) = w_{0} + w_{1}x_{1}+ \dots + w_{D}x_{D}\]with $\mathbf{x}$ in this simple case being $\mathbf{x} = (x_{1}, \dots, x_{D})^{T}$.
(i.e. a single observation per variable).
We can use linear regression to even predict the log of odds as follows:
\[log\left(\frac{p_{+}(\mathbf{x})}{1-p_{+}(\mathbf{x})}\right) = f(\mathbf{x}, \mathbf{w}) = w_{0} + w_{1}x_{1}+ \dots + w_{D}x_{D}\]where $p_{+}(\mathbf{x})$ represent the model’s estimate of the probability to belong to the positive class (e.g. $y = 1$)
💡 The log of odds function is known as the logit function: $logit(p) = log(\frac{p}{1-p})$
Since often we actually want the estimated probability of class membership, not the log of odds, we can solve the above equation for the $p_{+}$probability leading to the following - relatively ugly equation - of the positive class:
\[p_{+}(\mathbf{x}) = \frac{1}{1 + e^{-f(\mathbf{x})}}\]The same formula can be re-written using matrix notation (and even the basis notation saw in Linear Regression in my previous article) using the input data
\[p_{+}(\mathbf{x}) = \frac{1}{1 + e^{-f(\mathbf{x})}} = \frac{1}{1 + e^{-\mathbf{w^{T}x}}}\]Plotting the equation above leads to the well-known logistic (sigmoid) function.
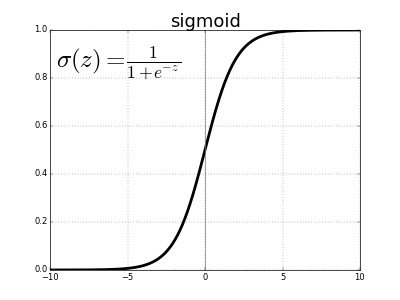
This curve is called a “sigmoid” curve because of its “S” shape which squeezes the probabilities into their correct range (between 0 and 1).
As you can see above, there is an association between the linear regression and logistic regression and can help us build intuition about their connection. As a result, we define the Logistic Regression model as:
\[f_{w}(\mathbf{x}) = \frac{1}{1 + e^{-\mathbf{w^{T}x}}}\]where $f_{w}(\mathbf{x})$ is the probability $p_{+}{(\mathbf{x})}$ that the instance belongs to the positive class.
Loss Functions
In Linear Regression we used the Mean Squared Error (MSE) as an objective function to minimize. On the other hand, in logistic regression we maximize the likelihood of our training set according to the model. In statistics, the likelihood function defined how likely the observation (an example) is according to our model.
We have defined the following relationship:
- If $y=1$ → $f_{w}(\mathbf{x})$
- If $y=0$ → $1 - f_{w}(\mathbf{x})$
It’s easy to derive the following unified equation:
\[L(w) = f_{w}(x_{i})^{y_i}(1-f_{w}(x_{i}))^{1-y_i}\]Maximum Likelihood Estimation
\[L(w) = \prod\limits_{i=1}^{N}f_{w}(x_{i})^{y_i}(1-f_{w}(x_{i}))^{1-y_i} \equiv \sum\limits_{i=1}^{N}[y_i log(f_{w}(x_i)) + (1-y_i) log(1-f_{w}(x_i))]\]
The equation is known as the Log-Loss and instead of maximising the following equation, we can safely add a $-$ sign and minimise the negative Log-Loss (or negative Log-Likelihood).
💡 In the context of binary classification, minimizing cross-entropy and minimizing log-loss are equivalent. Therefore, saying that you are minimizing either the cross-entropy or the log-loss in binary classification is essentially the same thing.
However, in the context of multi-class classification, cross-entropy and log-loss can have different interpretations and formulations. The cross-entropy loss for multi-class classification is also known as the softmax loss or negative log-likelihood loss. It is a more general measure of the difference between the predicted probabilities and the true labels, and is commonly used as the loss function for training neural networks. On the other hand, the log-loss is specific to binary classification and does not have a straightforward generalization to multi-class problems.
In general, we want to minimize the negative log-likelihood $-L(w)$ and we use to optimisation algorithms to make that happen:
- Batch gradient descent
- Newtons method
Note: derives to the solution quicker.
Model Evaluation
-
Accuracy:
Accuracy is the most commonly used metric for evaluating the performance of a classification model. It measures the proportion of correctly classified instances out of the total number of instances. While accuracy can be a useful metric, it may not be appropriate when the classes are imbalanced.
Accuracy = (TP + TN) / (TP + TN + FP + FN) -
Precision and Recall:
Precision and recall are metrics that are useful when the classes are imbalanced. Precision measures the proportion of true positive predictions out of all positive predictions, while recall measures the proportion of true positive predictions out of all actual positive instances. A trade-off between precision and recall can be made by adjusting the threshold for classification.
Precision = TP / (TP + FP)
Recall = TP / (TP + FN) -
F1 score:
The F1 score is the harmonic mean of precision and recall and is a useful metric when both precision and recall are important.
\(\text{F1 score} = 2*(\text{precision}* \text{recall}) / (\text{precision} + \text{recall})\) -
ROC curve and AUC:
The ROC curve is a plot of the true positive rate (TPR) against the false positive rate (FPR) at different threshold values. The area under the ROC curve (AUC) measures the performance of the model across all possible threshold values and is a commonly used metric for evaluating the performance of a binary classification model. -
Confusion matrix:
A confusion matrix is a table that summarizes the performance of a binary classification model. It shows the number of true positives, false positives, true negatives, and false negatives and can be used to calculate metrics such as accuracy, precision, recall, and F1 score.