The central limit theorem (CLT) is a powerful tool that allows us to make inferences about populations, even if we don’t know the exact distribution of the population. Just wave your wand (i.e., use the CLT) over a sample of data, and the distribution of the sample means will be approximately normally distributed, regardless of the shape of the population distribution.
Central Limit Theorem
-
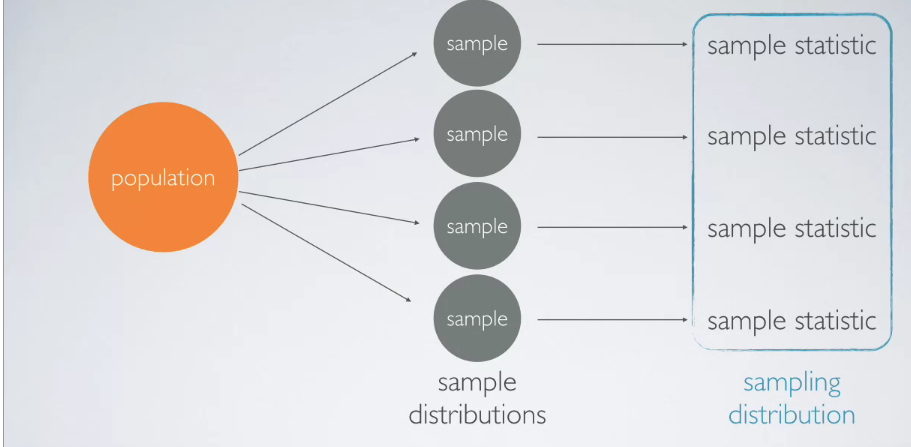
Population
The population of interest that we want to do some inference on (e.g. average height). - Sample
A large sample from the population (e.g. the height of 100 random people).
- Each of these samples, will have its own distribution (i.e. sample distribution).
-
Sample Statistic
A sample statistic is a single value that corresponds to the sample (e.g. mean).
- For each sample, we have a single 1-2-1 sample statistic. - Sampling Distribution
All of the sample statistics (e.g. means), have their own distribution named the sampling distribution.
Central Limit Theorem: The sampling distribution of the mean is nearly normally centred at the population mean, with standard error equal to the population standard deviation divided by the square root of the sample size.
$\hat{x} \space \approx N(\text{mean} = \mu, \text{SE} = \frac{\sigma}{\sqrt{n}})$
Conditions for the CLT:
-
Independence:
Sampled observations must be independent.
a. If sampling without replacement, $n <10$% of the population.💡 We don’t want to sample too large because it is highly likely that we will select an observation that is not independent.
E.g. If a take a sample of myself, if I have a too large sample size, it is likely I will also sample my mother/father etc. -
Sample size/skew:
a. Either the population distribution is normal.
b. Either the distribution is skewed, the sample size is large (rule of thumb: $n>30$).
CLT for means - Interactive examples
Layman’s term explanation
The Center Limit Theorem states that if any random variable, regardless of the distribution, is sampled a large enough times, the sample mean will be approximately normally distributed. This allows for studying the properties of any statistical distribution as long as there is a large enough sample size.
Applications in Data Science
The CLT is a powerful tool that can be used to make inferences about populations. It is an important theorem for data scientists to understand.
Here are some additional examples of how the CLT is used in data science:
-
Machine learning:
The CLT is used in machine learning algorithms such as linear regression, logistic regression, and support vector machines. -
Quality control:
The CLT is used to monitor the quality of products or services. For example, a company might use the CLT to ensure that the average weight of a bag of cereal is within a certain range. -
Finance:
The CLT is used to calculate the probability of certain financial events, such as the probability of a stock price going up or down.
The CLT is a versatile tool that can be used in a variety of different applications. It is an important theorem for data scientists to understand.